やさしい 建築構造力学演習問題集

実用的な解法を習得!2級建築士対策に最適
構造力学の学習には、手を動かして解く練習が不可欠だ。図や計算式を書き込みながら使える本書では、図解豊富な例題で解き方の本質を理解し、基礎から建築士試験レベルまで計200問以上の演習問題を通して実用的な解法を習得できる。単元ごとの見開き構成と別冊の解答解説で取り組みやすく、2級建築士受験対策の自習にも最適
浅野清昭 著
| 体裁 | B5判・144頁 |
|---|---|
| 定価 | 本体1400円+税 |
| 発行日 | 2018-08-05 |
| 装丁 | KOTO DESIGN Inc. 山本剛史 |
| ISBN | 9784761513689 |
| GCODE | 4059 |
| 販売状況 | 在庫◎ |
| 関連コンテンツ | レクチャー動画あり(全1件) |
| ジャンル | |
| 教科書分野 | |
| 教科書シリーズ | 図説やさしい(建築)シリーズ |
| 授業支援 |
まえがき
第1章 基礎計算
第2章 力の基礎
2・1 力
2・2 力のモーメント
2・3 合 力
2・4 分布荷重
チャレンジ問題01
第3章 力の釣り合い
3・1 平行な力
3・2 色々な方向の力
チャレンジ問題02
第4章 反 力
4・1 単純梁の反力
4・2 片持ち梁の反力
4・3 張り出し梁の反力
4・4 ラーメンの反力
チャレンジ問題03
第5章 部材に生じる力(基礎編)
5・1 単純梁(集中荷重)
5・2 単純梁(分布荷重)
5・3 単純梁(モーメント荷重)
5・4 片持ち梁
第6章 部材に生じる力(実戦編)
6・1 実用的解法
6・2 梁
6・3 ラーメン
6・4 3ヒンジラーメン
チャレンジ問題04
チャレンジ問題05
チャレンジ問題06
第7章 トラス
7・1 節点法
7・2 図解法
7・3 切断法
チャレンジ問題07
第8章 断面に関する数量
8・1 図心・断面1次モーメント
チャレンジ問題08
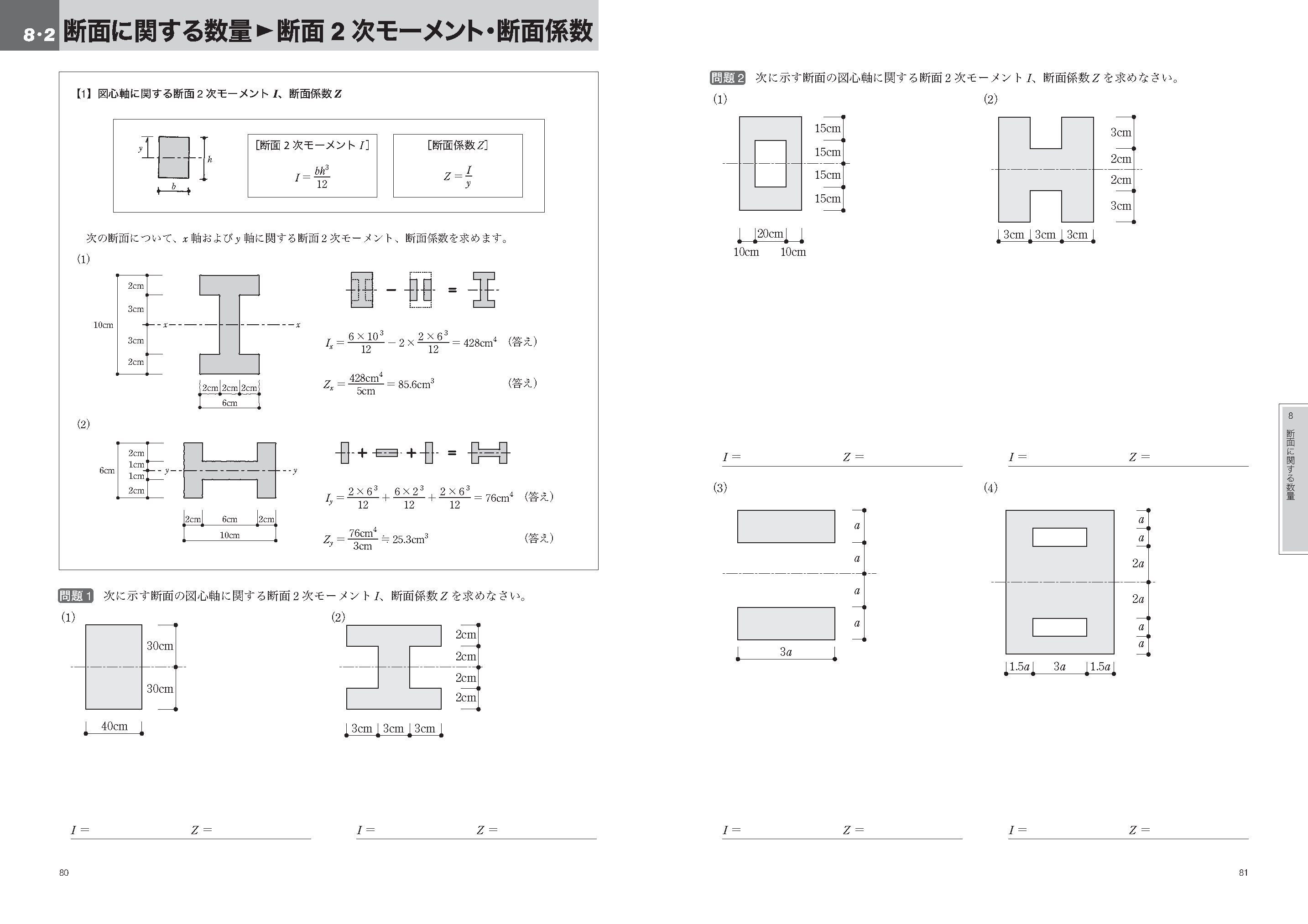
8・2 断面2次モーメント・断面係数
チャレンジ問題09
第9章 応力度
9・1 軸応力度・伸び
9・2 曲げ応力度・せん断力度
9・3 許容応力度
チャレンジ問題10
チャレンジ問題11
チャレンジ問題12
9・4 組合せ応力度
第10章 座 屈
10・1 座 屈
チャレンジ問題13
チャレンジ問題14
第11章 たわみ
11・1 たわみ・たわみ角公式
チャレンジ問題15
11・2 たわみの求め方
第12章 不静定構造の基礎
12・1 モーメント荷重
12・2 中間荷重
第13章 塑性解析の基礎
13・1 静定構造
13・2 不静定構造
別冊 解答・解説
構造力学を学習していく上で、自分の手を動かして解く作業は欠かせません。講義を聞いて「わかった」と思っても、実際に解いてみると「あれ? どうだったっけ?」となってしまうからです。自分の力で何度も解く練習をして初めて構造力学は自分のものになるのです。そのため、構造力学の講義には、問題を解く教材が不可欠なのです。そこでこのたび、本書「やさしい 建築構造力学 演習問題集」を作成いたしました。本書が構造力学学習の良きパートナーになれば幸いです。
[本問題集の特長]
- 高等数学不要…………第1章・基礎計算で紹介している程度の数学で取り組めます。
- シンプルな問題………解法の本質を理解していただくためには複雑な問題は要りません。シンプルで、気持ちよく解けるように工夫しています。「解ける喜び」を感じていただき、理解へと結びつけてください。
- イラストでの解説……解法の解説ページを設けました。解説にはイラストを使い、力を実感できるように工夫しています。
- 実用的な解法…………「スパナ化法」「面積法」なども取り上げ、問題を見ただけで応力図が目に浮かぶようになることをめざしてください。
- チャレンジ問題………建築士資格試験の問題を意識した〈チャレンジ問題〉を用意しました。各パートを理解できたら、トライしてみましょう。
[問題を解くにあたっての注意点]
- 計算式は丁寧にたてましょう。横着すると上達しませんよ。
- 必要に応じて図を描きましょう。今自分が解こうとする対象物をはっきりさせることが大切です。
- 力の釣り合い式にはΣX=0などの目印となる記号を書いておきましょう。復習するときに自分のたてた式が何なのか一目でわかります。
- 暗算しない! 面倒臭さがらず丁寧に式を展開し、符号間違いなどのうっかりミスをなくしましょう。
- 答えには必ず単位を書きましょう。物理量には単位が必要です。
本書を通して構造力学に親しんでいただき、みなさんそれぞれの目標を達成していただければ、著者にとってこのうえない喜びです。
平成30年6月30日
浅野 清昭
本書に下記の誤りが含まれておりました。お詫びして訂正いたします。
本体110ページに記載の発行日をお確かめのうえ、お手持ちのバージョンに合ったものをご覧ください。
最終更新:2024年11月18日
第4版第1刷(2024年3月20日発行)用 正誤表
第3版第1刷(2021年6月20日発行)用 正誤表
第2版第1刷(2020年2月20日発行)用 正誤表
第1版第1刷(2018年8月5日発行)用 正誤表
補足Q&A
- p.20[4.1 反力▶単純梁の反力]【3】モーメント荷重の場合〈point〉欄などに記載の「そのまま」の意味は?
- 「距離を掛け合わせることなく、そのままのモーメント荷重の値(時計回り+、反時計まわりーとして)をΣM=0の式に入れる。」という意味です。モーメント荷重に距離を掛けてしまう人が多いので、pointとして記しています。
教科書をお探しの先生方へ
採用検討用見本ご請求フォーム
ご入力前にご確認ください
- ブラウザとして「Safari」をご利用の場合、送信を完了できない可能性がございます。Chrome、Firefox、Edgeなどのご利用をおすすめします。
- 「@outlook.com」「@hotmail.com」「@msn.com」「@icloud.com」ドメインのメールアドレスは、当サイトからのメールを正しく受信いただけない場合がございます。
お問い合わせ
ご入力前にご確認ください
- ブラウザとして「Safari」をご利用の場合、送信を完了できない可能性がございます。Chrome、Firefox、Edgeなどのご利用をおすすめします。
- 「@outlook.com」「@hotmail.com」「@msn.com」「@icloud.com」ドメインのメールアドレスは、当サイトからのメールを正しく受信いただけない場合がございます。